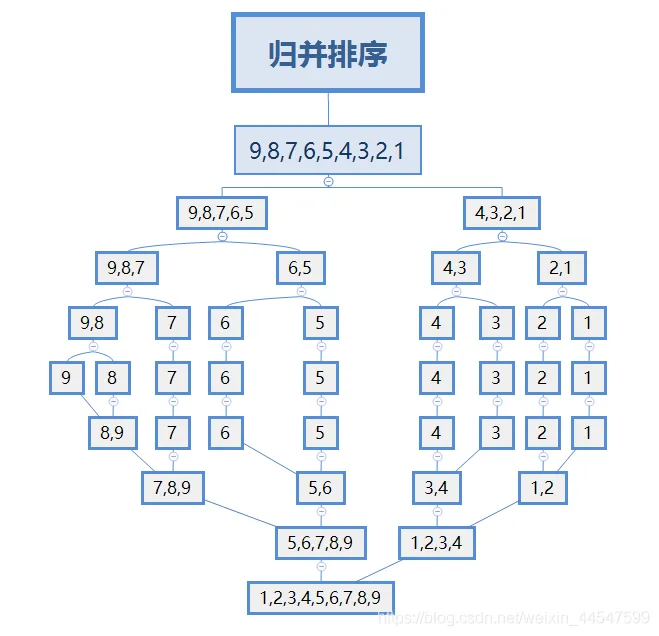
归并排序是建立在归并操作上的一种有效、稳定的排序算法，该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

TIP

1. 将一个数组拆分为两个，从中间点拆开，通过递归操作来实现一层一层拆分。
2. 从左右数组中选择小的元素放入到临时空间，并移动下标到下一位置。
3. 重复步骤2直到某一下标达到尾部。
4. 将另一序列剩下的所有元素依次放入临时空间。
5. 将临时空间的数据依次放入原数据数组。

编码实现

public class MergeSort {

    private MergeSort() {
    }

    public static <E extends Comparable<E>> void sort(E[] arr) {
        sort(arr, 0, arr.length - 1);
    }

    private static <E extends Comparable<E>> void sort(E[] arr, int l, int r) {
        if (l >= r) {
            return;
        }

        int mid = l + (r - l) / 2;
        sort(arr, l, mid);
        sort(arr, mid + 1, r);
        merge(arr, l, mid, r);
    }

    /**
     * 合并两个有序区间 arr[l,mid] 和 arr[mid+1, r]
     *
     * @param arr 数组
     * @param l   左侧索引
     * @param mid 数组分割处
     * @param r   右侧索引
     * @param <E> 数组类型
     */
    private static <E extends Comparable<E>> void merge(E[] arr, int l, int mid, int r) {
        // 拷贝数组[l,r+1]，因为copyOfRange是拷贝[l,r)所以要r+1
        E[] temp = Arrays.copyOfRange(arr, l, r + 1);

        // i指向[l,mid]的第一个元素，j指向[mid+1, r]中的第一个元素
        int i = l, j = mid + 1;

        for (int k = l; k <= r; k++) {
            if (i > mid) {
                // 左边所有元素都取完了，就去取右边
                arr[k] = temp[j - l];
                j++;
            } else if (j > r) {
                // 右边所有元素都取完了，就去取左边
                arr[k] = temp[i - l];
                i++;
            } else if (temp[i - l].compareTo(temp[j - l]) <= 0) {
                // 左边更小一点
                arr[k] = temp[i - l];
                i++;
            } else {
                // 右边更小一点
                arr[k] = temp[j - l];
                j++;
            }
        }
    }
}