优先队列的出队顺序只和优先级有关和入队顺序无关，比如每次出队都是数据中的最大值。如果直接使用数组，无论是取数据还是插入数据时进行排序，都会有一个步骤的时间复杂度是O(n)级别的，本文借助二叉堆实现优先队列。

二叉堆

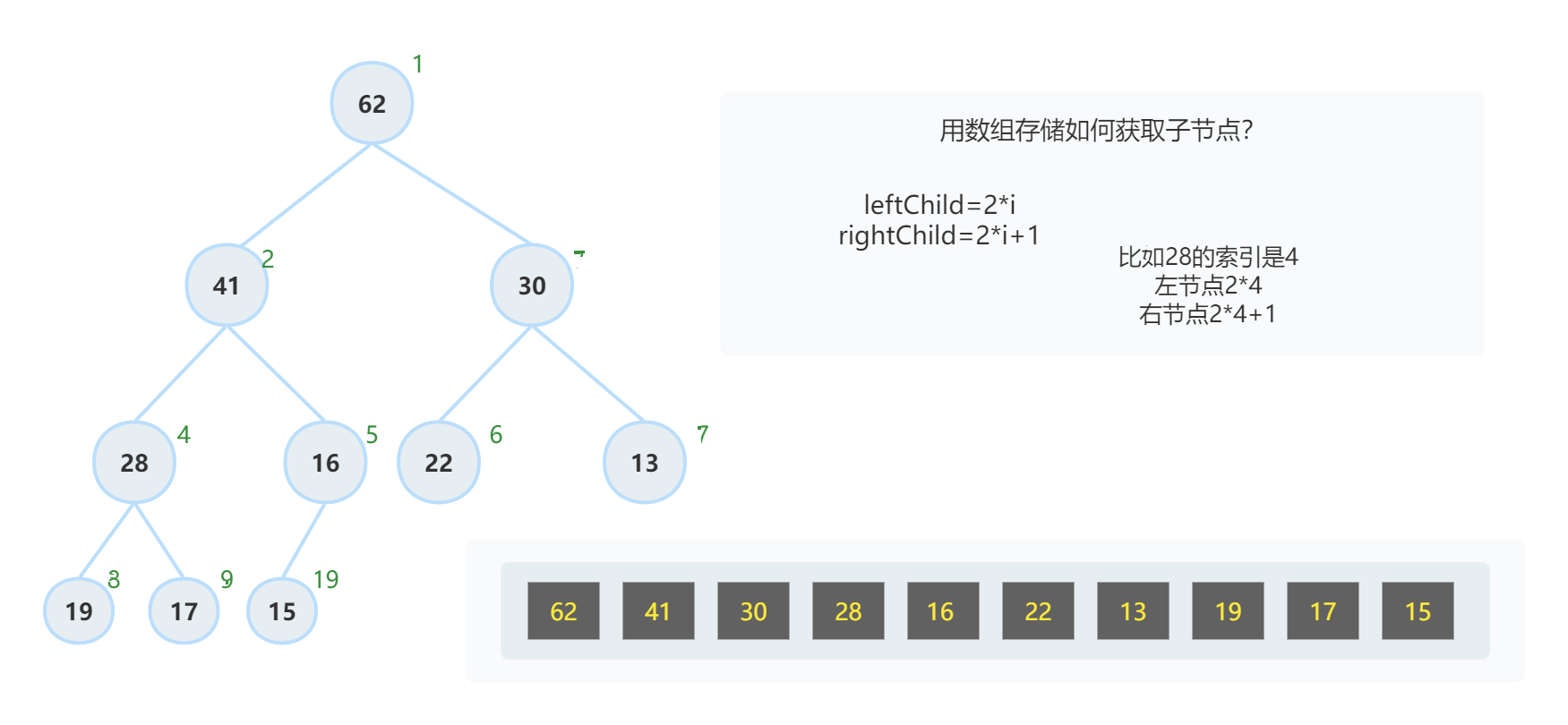
二叉堆本质上是一种完全二叉树，它分为两个类型：最大堆和最小堆，下面举例说明最大堆

1. 父节点一定比子节点大
2. 第4行不一定比第3行小，例如第三行的13才是整个树中最小的元素
3. 用数组存储如何获取子节点？leftChild=2*i，rightChild=2*i+1
   1. 但实际上索引是从1开始的，左节点应该是leftChild=2*i+1，右节点rightChild=2*i+2，父节点parent(i)=(i-1)/2

最小堆和最大堆相似，就不细写了

定义最大堆基本结构

public class MaxHeap<E extends Comparable<E>> {
    private ArrayList<E> data;

    public MaxHeap(int capacity) {
        data = new ArrayList<>(capacity);
    }

    public MaxHeap() {
        data = new ArrayList<>();
    }

    public int getSize() {
        return data.size();
    }

    public boolean isEmpty() {
        return data.isEmpty();
    }
}

查询父节点、左右子节点索引

public class MaxHeap<E extends Comparable<E>> {
    // 返回父节点的索引
    private int parent(int index) {
        if (index == 0) throw new IllegalArgumentException("此项无父节点");
        return (index - 1) / 2;
    }

    // 返回左子节点的索引
    private int leftChild(int index) {
        return index * 2 + 1;
    }

    // 返回右子节点的索引
    private int rightChild(int index) {
        return index * 2 + 2;
    }
}

向堆中添加函数SiftUp

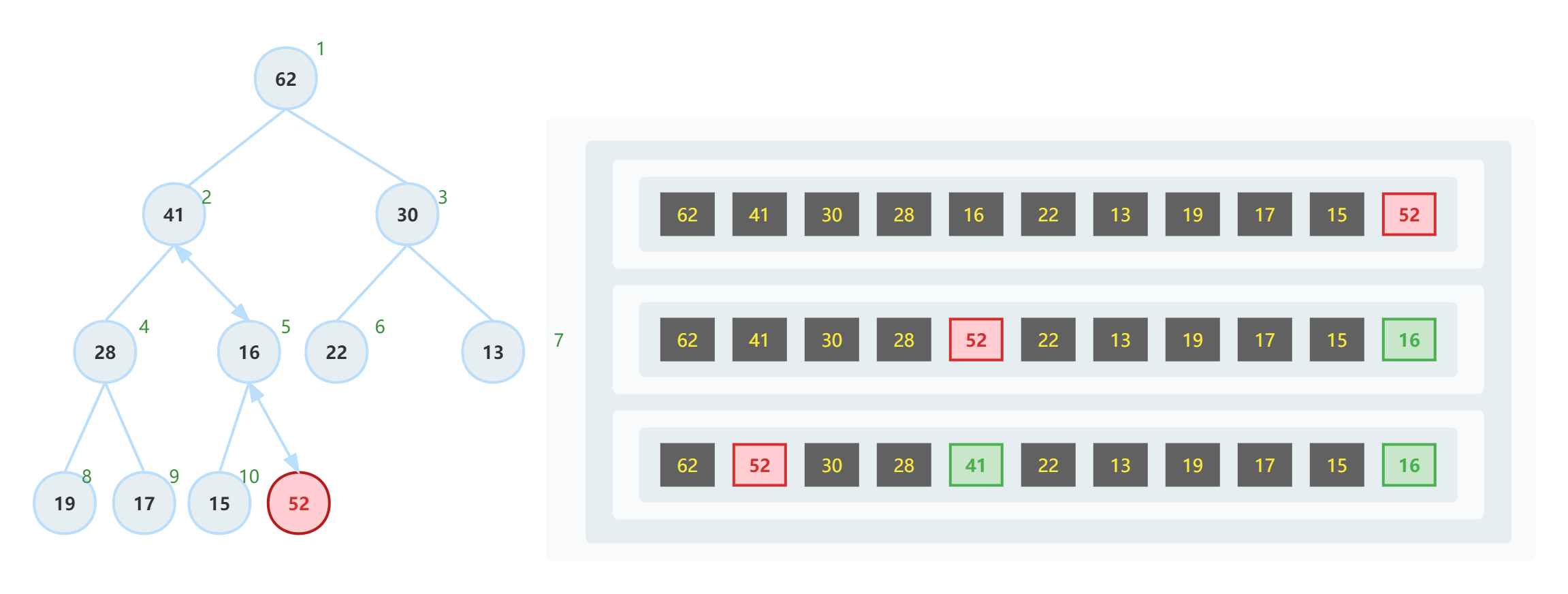
在数组尾添加一个元素52，找到其父节点，如果父节点小于52则交换子父节点，一直进行直到找到父节点大于子节点或到树根为止。

public class MaxHeap<E extends Comparable<E>> {
    
    private ArrayList<E> data;

    // 返回父节点的索引
    private int parent(int index) {
        if (index == 0) throw new IllegalArgumentException("此项无父节点");
        return (index - 1) / 2;
    }

    // 添加元素
    public void  add(E e) {
        data.add(e);
        siftUp(data.size() - 1);
    }

    private void siftUp(int k) {
        while (k>0 && data.get(parent(k)).compareTo(data.get(k)) == 0) {
            Collections.swap(data,k,parent(k)); // 交换位置
        }
    }
}

取出最大堆中元素

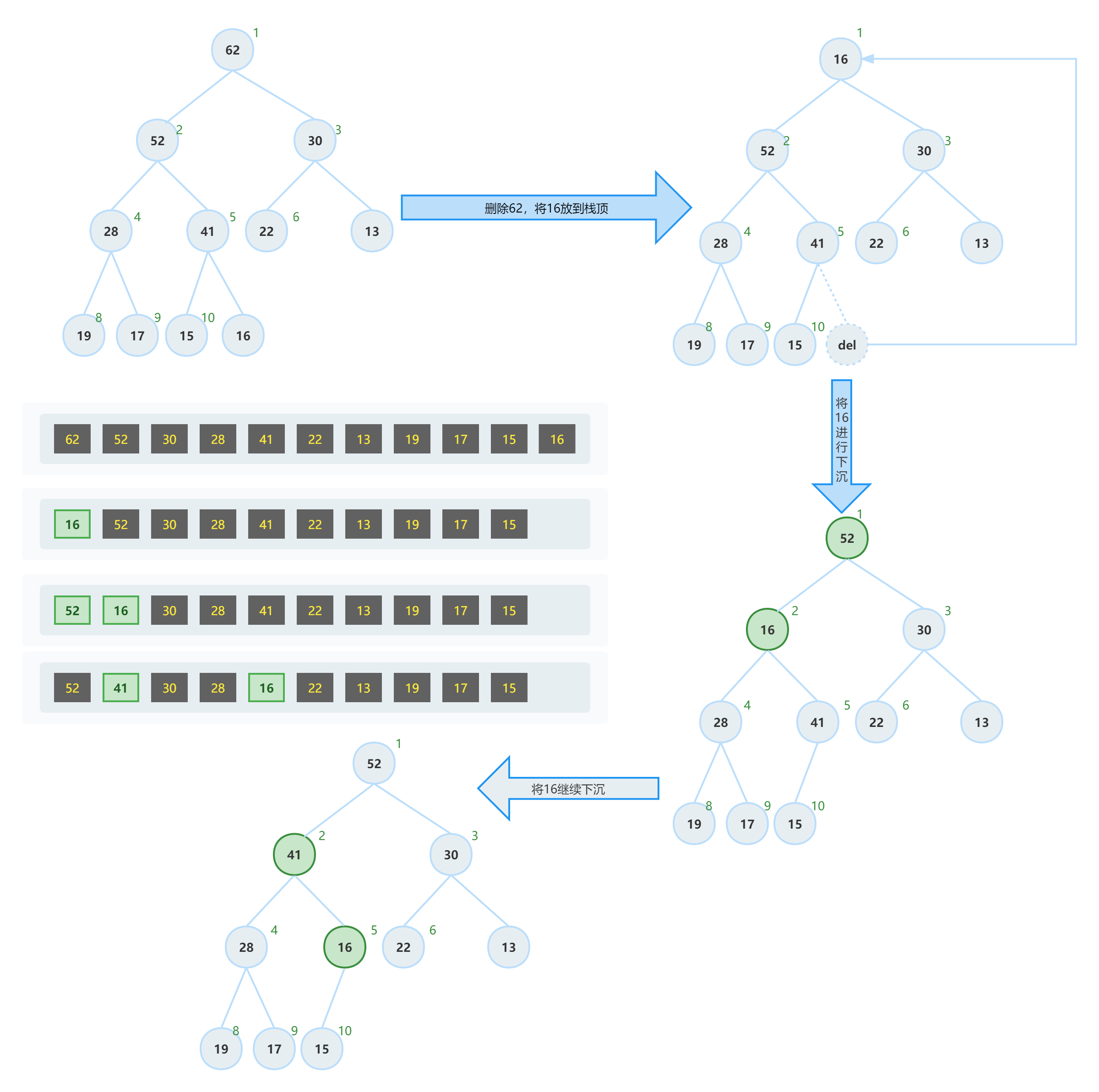
1. 获取堆顶元素，也就是数组下标为0的元素，作为方法的返回值
2. 数组下标为0的元素值更改为数组最后一个元素的值，然后删除最后一个元素
3. 对此时的元素进行“下沉操作”，如果比左/右子树小，则和教大的那个元素更换位置。

public class MaxHeap<E extends Comparable<E>> {
    // 获取堆中最大元素
    public E findMax() {
        if (data.size() == 0) {
            throw new IllegalArgumentException("获取失败，数组为空");
        }
        return data.get(0);
    }

    // 取出最大元素
    public E extractMax() {
        E ret = findMax();
        // 1.堆顶和最后一个元素交换位置
        Collections.swap(data, 0, data.size() - 1);
        // 2.删除堆尾元素
        data.remove(data.size() - 1);
        // 3.下沉元素
        siftDown(0);
        return ret;
    }

    // 元素下沉
    private void siftDown(int k) {
        // 左子节点索引<数组长度，也就是数组没有遍历完毕，则进入循环
        while (leftChild(k) < data.size()) {
            // j默认存储左节点
            int j = leftChild(k);
            // j+1代表右子节点，右节点<数组长度（保障数组右节点有数据）
            if (j + 1 < data.size() && data.get(j + 1).compareTo(data.get(j)) > 0) {
                // 如果右节点 > 左节点，则j等于右节点
                j = rightChild(k);
            }
            // 此时data[j]是左右节点中的最大值，如果data[k]>最大值，则结束循环
            if (data.get(k).compareTo(data.get(j)) >= 0) {
                break;
            }
            // 否则交换位置
            Collections.swap(data, k, j);
            k = j;
        }
    }
}

排序实战应用篇之堆排序

逻辑很简单，先存入到最大堆中去，然后再取出赋值给数组data。

public class HeapSort {
    private HeapSort() {}

    public static <E extends Comparable<E>> void sort(E[] data) {
        MaxHeap<E> maxHeap = new MaxHeap<>();
        for (E e : data) {
            maxHeap.add(e);
        }
        for (int i = 0; i < data.length; i++) {
            data[i] = maxHeap.extractMax();
        }
    }
}

分析：add的复杂度是O(n)*extractMax复杂度O(logn)，因此上述代码的时间复杂度是O(nlogn)，下面介绍一种改进的堆排序，时间复杂度为O(n)

堆的replace操作

删除即将出堆的元素，也就是当前堆顶数组下标为0的元素，然后插入一个元素。这个实现起来也很简单，将新元素设置为堆顶值，然后对堆顶进行“下沉”操作。

public class MaxHeap<E extends Comparable<E>> {
    public E replace(E e) {
        E ret = findMax();
        data.set(0, e);
        siftDown(0);
        return ret;
    }
}

​

将任意数组整理成堆的形状

实现思路：从叶子节点开始进行上浮操作

public class MaxHeap<E extends Comparable<E>> {
    
    private ArrayList<E> data;
    
    public MaxHeap(ArrayList<E> arr) {
        data = new ArrayList<E>(arr);
        for (int i = data.size() - 1; i > 0; i--) {
            siftDown(i);
        }
    }
}

思考：上面提到过的堆排序，是使用for循环插入元素，使用这种方式直接插入数组是不是更好？为什么？

基于堆的优先队列

上面我们实现了最大堆，最大堆天然支持优先队列的功能，接下来我们着手实现一下，首先来看之前写过的对队列接口的定义

public interface Queue<E> {
    int getSize();
    boolean isEmpty();
    void enqueue(E e);
    E dequeue();
    E getFront();
}

优先队列

public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {

    private MaxHeap<E> maxHeap;

    public PriorityQueue() {
        this.maxHeap = new MaxHeap<>();
    }

    @Override
    public int getSize() {
        return maxHeap.getSize();
    }

    @Override
    public boolean isEmpty() {
        return maxHeap.isEmpty();
    }

    @Override
    public void enqueue(E e) {
        maxHeap.add(e);
    }

    @Override
    public E dequeue() {
        return maxHeap.extractMax();
    }

    @Override
    public E getFront() {
        return maxHeap.findMax();
    }
}