Appearance
二分搜索树又称二分排序树,它具有很多优异的性质,能快速完成特定场景下的需求,同时也是一个很好的联系递归思维的数据结构。
- 根节点:最顶层的节点
- 叶子节点:最底层的节点
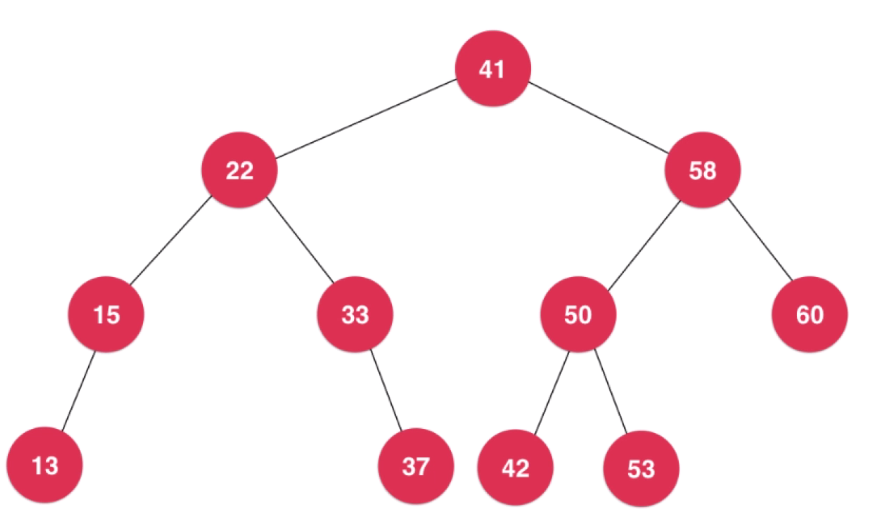
基本结构
新建一个BST类,二分搜索树的底层是链表,其中子类Node来表示链表结构,BST维护root根节点和树的大小。
java
public class BST<E extends Comparable<E>> {
private class Node {
public E e;
public Node left, right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
private Node root;
private int size;
public BST() {
root = null;
size = 0;
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
}二分搜索树的添加方法
首先来看添加操作,如果树为空则添加根节点,否则进行下一步操作,具体看注释。
java
public class BST<E extends Comparable<E>> {
public void add(E e) {
root = add(root, e);
if (root == null) {
root = new Node(e);
size++;
}else {
add(node,e);
}
}
private void add(Node node, E e) {
if (node.e.equals(e)) {
return; // 1.如果相等,则不进行添加
} else if (e.compareTo(node.e) < 0 && node.left == null) { // 2.如果 e<node.e 且左子树为空,则新建到左子树
node.left = new Node(e);
size++;
} else if (e.compareTo(node.e) > 0 && node.right == null) { // 3.如果 e>node.e 且右子树为空,则新建到叶子节点
node.right = new Node(e);
size++;
} else if (e.compareTo(node.e) < 0) { // 4.如果 e<node.e,则递归调用左子树,直到遍历到叶子节点
add(node.left, e);
} else {
add(node.right, e); // 4.如果 e>node.e,则递归调用右子树,直到遍历到叶子节点
}
}
}二分搜索树的添加方法改进
上述的方法有没有问题?首先添加操作需要额外对添加根节点进行判断,下面介绍一种更加优雅的方法,不但能解决这个问题,还能使得代码更加简洁。
java
public class BST<E extends Comparable<E>> {
public void add(E e) {
root = add(root, e);
}
// 添加方法改进版
private Node add(Node node, E e) {
if (node == null) {
size++;
return new Node(e);
}
if (e.compareTo(node.e) <= 0) {
node.left = add(node.left, e); //宏观理解方式:对node.left进行重新赋值,这是通过递归得到包含新数据的树
} else if (e.compareTo(node.e) > 0) {
node.right = add(node.right, e);
}
return node;
}
}是否包含某数据
同样是采用递归实现,如果比node节点大就去右子树找,如果比node节点小就去左子树找,找到最后如果为null就是不包含。
java
public class BST<E extends Comparable<E>> {
public boolean contains(E e) {
return contains(root, e);
}
private boolean contains(Node node, E e) {
if (node == null) {
return false;
}
if (e.compareTo(node.e) == 0) {
return true;
}
if (e.compareTo(node.e) < 0) {
return contains(node.left, e);
} else {
return contains(node.right, e);
}
}
}二分搜索树的前序遍历
二分搜索树的前序遍历的记忆法则是“根左右",即先遍历根节点,再遍历左子树节点,再遍历右子树节点。递归实现起来很容易,三步即可解决,先输出数据,然后递归左子树,最后递归右子树。
java
public class BST<E extends Comparable<E>> {
public void preOrder() {
preOrder(root);
}
private void preOrder(Node node) {
if (node == null) {
return;
}
System.out.print(node.e+"\t");
preOrder(node.left);
preOrder(node.right);
}
}二分搜索树的中序与后序遍历
有了前序遍历的基础,中序与后序也很简单,相对而言计算机领域常考的是其遍历结果,不过这不是本篇文章的重点,就不过多赘述了。
java
public class BST<E extends Comparable<E>> {
/** 二分搜索树中序遍历 */
public void inOrder() {
inOrder(root);
System.out.println();
}
private void inOrder(Node node) {
if (node == null) {
return;
}
inOrder(node.left);
System.out.print(node.e+"\t");
inOrder(node.right);
}
/** 二分搜索树后序遍历 */
public void postOrder() {
postOrder(root);
System.out.println();
}
private void postOrder(Node node) {
if (node == null) {
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.print(node.e+"\t");
}
}注意看中序遍历的数据,发现是有序的。
二分搜索树遍历的测试
java
public static void main(String[] args) {
BST<Integer> bst = new BST<>();
///////////////////////
// 5 //
// / \ //
// 3 6 //
// / \ / \ //
// 2 4 8 //
// / //
// 7 //
///////////////////////
int[] nums = {5, 3, 6, 8, 4, 2, 7};
for (int num : nums) {
bst.add(num);
}
System.out.print("前序遍历:");
bst.preOrder();
System.out.print("中序遍历:");
bst.inOrder();
System.out.print("后序遍历:");
bst.postOrder();
}测试结果:
shell
前序遍历:5 3 2 4 6 8 7
中序遍历:2 3 4 5 6 7 8
后序遍历:2 4 3 7 8 6 5重写二分搜索树的toString方法
为了方便测试,这里简单重写下toString方法,将树的深度遍历出来,效果没有上述注释部分表示的明显。
java
public class BST<E extends Comparable<E>> {
@Override
public String toString() {
StringBuffer res = new StringBuffer();
generateBSTString(root, 0, res);
return res.toString();
}
private void generateBSTString(Node node, int depth, StringBuffer res) {
if (node == null) {
res.append(generateDepthString(depth) + "null\n");
return;
}
res.append(generateDepthString(depth) + node.e + "\n");
generateBSTString(node.left, depth + 1, res);
generateBSTString(node.right, depth + 1, res);
}
private String generateDepthString(int depth) {
StringBuffer res = new StringBuffer();
for (int i = 0; i < depth; i++) {
res.append("--");
}
return res.toString();
}
}效果如下
java
5
--3
----2
------null
------null
----4
------null
------null
--6
----null
----8
------7
--------null
--------null
------null获取二分搜索树的最小值与最大值
二分搜索树有两个性质,①若它的左子树不为空,则左子树上所有节点的值都小于根节点的值;②若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
根据二分搜索树的性质不难得到,最左侧底部的叶子节点就是二分搜索树的最小值,最右侧底部的叶子节点就是二分搜索树的最大值,根据递归获取到二分搜索树的最小值与最大值。
java
public class BST<E extends Comparable<E>> {
public E minimum() {
if (size == 0){
throw new IllegalArgumentException("当前序列无数据");
}
return minimum(root).e;
}
private Node minimum(Node node) {
if (node.left == null) {
return node;
}
return minimum(node.left);
}
}上述代码是获取二分搜索树的最小值,下面是获取二分搜索树的最大值
java
public class BST<E extends Comparable<E>> {
public E maximum() {
if (size == 0){
throw new IllegalArgumentException("当前序列无数据");
}
return maximum(root).e;
}
private Node maximum(Node node) {
if (node.right == null) {
return node;
}
return maximum(node.right);
}
}删除二分搜索树的最大值与最小值
删除最小值不难,由于最小值的左子树一定为空,如果左子树不为空说明它不是最小的,这个不难理解。但是最小值的右子树可能不为空,这样的情况下,我们需要将最小值的右子树根节点代替最小值的位置,这样就完成了删除最小值。
java
public class BST<E extends Comparable<E>> {
public E removeMin() {
// 找到最小值
E ret = minimum();
root = removeMin(root);
return ret;
}
private Node removeMin(Node node) {
// 当子节点的左子树为null时,说明当前节点就是最小值
if (node.left == null) {
// 将要删除节点的右子树,代替删除节点的位置,右子树为空也没有关系,不影响
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
}删除最大值与删除最小值相似,只不过需要考虑最大值左子树不为空的情况。
java
public class BST<E extends Comparable<E>> {
public E removeMax() {
// 找到最大值
E ret = maximum();
root = removeMax(root);
return ret;
}
private Node removeMax(Node node) {
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
}删除二分搜索树的任意值
有了删除最大值与最小值的基础,被删除的节点无论是左子树为空还是右子树为空,处理方法和删除最大最小值相似。难点在于左右子树都不为空的情况,将当前节点设置为右子树的最小节点,挂载到当前节点的位置。
java
public class BST<E extends Comparable<E>> {
public void remove(E e) {
remove(root, e);
}
private Node remove(Node node, E e) {
if (node == null) {
return null;
}
if (e.compareTo(node.e) < 0) {
// 如果 e<node.e 则当前节点去左子树去找
node.left = remove(node.left, e);
return node;
} else if (e.compareTo(node.e) > 0) {
// 如果 e>node.e 则当前节点去右子树去找
node.right = remove(node.right, e);
return node;
} else {
// 相等的情况,开始删除逻辑
if (node.left == null) {
// 左子树为空,将右子树挂载到当前节点,删除当前节点
Node rightNode = node.right;
node.right = null;
size--;
// 理解递归逻辑,直接返回右子树相当于完成了挂载逻辑
return rightNode;
}
if (node.right == null) {
// 右子树为空,将左子树挂载到当前节点,删除当前节点
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 左右子树都不为空,将当前节点设置为右子树的最小节点,挂载到当前节点的位置
Node successor = minimum(node.right); // 获取右子树最小值
// 以successor为根节点,右子树就是删除右子树最小值后的node节点
successor.right = removeMin(node.right);
// 以successor为根节点,左子树是不变的
successor.left = node.left;
// 原节点置空,交给GC处理
node.left = node.right = null;
return successor;
}
}
}扩展:非递归实现前序遍历
非递归需要借助”栈“数据结构,详细代码如下:
java
public void preOrderNT() {
Stack<Node> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null)
stack.push(cur.right);
if (cur.left != null)
stack.push(cur.left);
}
}扩展:二分搜索树的层序遍历
层序遍历,顾名思义就是一层层的遍历,借助”队列“数据结构实现。
java
public void levelOrder() {
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
Node cur = queue.remove();
System.out.println(cur.e);
if (cur.left != null) {
queue.add(cur.left);
}
if (cur.right != null) {
queue.add(cur.right);
}
}
}TIP
思考:根据层序遍历实现加强版toStringPlus方法,采用树状形式显示,难点在于空格的显示。
